Matematik Neden Zor?
Nihat BOZ*
*
Gazi Üniversitesi, Gazi Eğitim Fakültesi Ortaöğretim Fen ve Matematik Alanları Eğitimi
Bölümü, Matematik Eğitimi Anabilim Dalı, Beşevler/Ankara, boz@gazi.edu.tr
Makale Gönderme Tarihi: 26 Mayıs 2008 Makale Kabul Tarihi: 17 Kasım 2008
Özet – Bu makalede, ülkemizde uygulanmaya başlanan yeni matematik müfredatlarının beslendiği fikirler ele
alınmış ve bu fikirlerin matematiğin gerçekte zor bir bilim olmadığı varsayımına dayandığı gösterilmeye
çalışılmıştır. Bütün bunlar literatüre dayandırılarak ele alınmıştır..Literatürde matematiğin doğası hakkındaki
görüşler tartışmanın mihenk taşını oluşturmuştur. Ernest (1989) matematiğin doğası hakkındaki görüşleri üç ana
kategoriye ayırır: Enstrümantalist, Platonist ve Problem-çözme. Bunlardan platonist ve problem-çözme görüşü
yapılandırmacı fikrin eğitim ve öğrenim anlayışına yakındır. Bu anlayış ile sunulan matematiğin öğrencilere
daha faydalı olacak ve onlar matematiği zor bir ders olarak görmeyeceklerdir. Bu iddia ülkemizde yapılan
çalışmalarla desteklenmiştir.
Anahtar kelimeler: Matematiğin doğası, yapılandırmacı eğitim, kavramsal anlama, ezbere dayalı öğrenim.
Why is Mathematics Difficult?
Abstract –In this paper, the views on new mathematics curriculum that began to be applied recently in our
country and that the views mentioned depends on the hypothesis that mathematics is not a difficult science were
discussed. All of these discussions were based on the literature. The beliefs on the nature of mathematics in
related literature were the vital points of these discussions. Ernest (1989) divides the beliefs on the nature of
mathematics into three categories: Instrumentalist, Platonist and Problem-Solving. Among those, Platonist and
problem-solving views are close to constructivist view of teaching and learning. The mathematics that is
presented with this view would be more beneficial to the students and they would not regard mathematics as a
difficult subject. This claim was supported by the research carried out in our country.
Key words: Nature of mathematics, constructivist teaching, conceptual understanding, rote learning..Boz, N 53
Giriş
2003 yılında 46 ülkedeki, 4. ve 8. sınıf öğrencilerinin matematikteki başarısını standart
testlerle ölçen uluslararası bir araştırma, çocukların başarı ortalamasının %50’ nin altında
olduğunu göstermiştir (URL 1). Bu kimilerine göre yeterli derecede başarı sayılabilir. Bu fikri
savunurken de herkesin matematiği öğrenmesine gerek yoktur gibi bir öneri getirebilirler.
Gerçekten, İngiltere’de bazı dönemlerde matematiğin cebri ilgilendiren bölümleri (harfli
ifadeler, denklem çözme vs.) öğrencilere zorunlu koşulmamıştı (Gray, şahsi görüşme). Bir
kısım eğitim teorisyenleri de Gardner’in (1993) ‘çoklu zekâ’ teorisinden yola çıkarak, her
öğrencinin matematikte başarılı olması gerekmez diye bir iddiada bulunabilirler.
Bu fikirlerin aksine, Poisson (1781–1840) matematiğin önemini vurgulamak için
”Hayatta yaşamaya değer iki şey vardır; matematiği keşfetme ve matematiği öğretme.”
demiştir. (1991). Bu fikre paralel görüşler günümüzde egemen olmaya başlamıştır. Bu
nedenle, matematik disiplini her öğrenciye kazandırılmalıdır görüşü geçerliliğini
korumaktadır. Hatta Amerika’da ‘Mathematics for All, Herkes için Matematik’ prensibinden
kaynaklanan çalışmalar olabildiğince yoğunlukta devam etmektedir. Bunun nedeni ise baş
döndürücü teknolojik gelişmelerin devam edebilmesi ve bunların kullanılabilmesi için
gerekenlerin matematik bilgisine ihtiyaç duymasıdır. Bu nedenle, çocuklarımıza en azından
temel matematiksel bilgi sunulması hala geçerliliğini korumaktadır. Bu nedenle, matematik
müfredatlarında yapılan değişiklikler bu doğrultuda atılmış adımlardan biri olarak görülebilir.
Matematiğin Doğası
Ernest (1989), matematiğin doğası hakkındaki görüşleri üç ana kategoriye ayırmıştır:
Enstrümantalist, Platonist ve Problem-çözme. Enstrümentalist görüşe göre matematik
gerçeklerin, kuralların ve becerilerin birikimidir. Platonist fikre göre matematik keşfedilmiş
statik fakat birbiriyle ilgili bilgilerin birleşimdir. Problem-çözme ise matematiği sürekli
gelişen dinamik, insanlarca yaratılan ve keşfedilen bir bilim olarak görür. Bu görüşlerden,
platonist ve problem çözme yapılandırmacı eğitim anlayışına yakındır. Platonist görüş
anlamanın aktif inşasını ön plana çıkarır. Problem-çözme ise bu fikrin yanında bireyin kendi
ilgisi doğrultusunda matematik bilgisinin inşasını savunur. Yani problem-çözme daha çok
birey merkezlidir. Beswick (2005), matematiğin doğası, matematik öğretimi ve öğrenimi
hakkındaki inançları tartışırken matematiğin doğası hakkındaki görüşler ile matematiğin
öğrenim ve öğretimi ile ilgili görüşlerin teorik bakımından birbirine bağlı olduğunu belirtiyor.
Necatibey Eğitim Fakültesi Elektronik Fen ve Matematik Eğitimi Dergisi 54 MATEMATİK NEDEN ZOR?
Fisher ve Ziebur (1965)’un yazdığı genel matematik kitabında, matematiğin
çıkarsamaya dayalı bir bilim olduğu belirtiliyor; yani matematiksel sonuçlar, başka sonuçlara
dayandırılarak, yani tümdengelimle çıkarılıyor. Bu aslında matematiğin düşünmeye dayalı bir
bilim olduğunu gösteriyor. Bazı matematikçilere göre, matematik beynin en karanlık
fakültelerini çalıştırmaya gereksinim duyar. ‘...dünyadaki hiçbir çalışma matematik kadar,
beynin bütün fakültelerini ahenkli bir şekilde çalışmasını sağlayamaz…’ (Sylvester, 1869).
Bu nedenle, matematiğin güzelliği, zihinsel uğraşlara davetiye çıkarmasındandır. Ünlü bir
bilim adamı olan Rényi (1970) ‘Kendimi mutsuz hissedersem, mutlu olmak için matematik
çalışırım. Kendimi mutlu hissedersem, bu mutluluğun sürmesi için matematik
çalışırım.’demiştir. Bu nedenle matematik aslında çok zevkli bir bilim dalıdır.
Matematiksel örüntüler ve ilişkiler matematiğin dili sayesinde gün yüzüne çıkıyor ve
insanoğlunun hizmetine sunuluyor. Matematik sayesinde bu örüntüleri ve ilişkileri
genelleyebiliyoruz. Matematiğin doğasında, örüntü ve ilişkilerin, birkaç tane durumundan
genelleme yapmak vardır. Hatta bazı matematikçilere göre matematik genellemelerden
ibarettir. Bu genellemelere varmada özel durumların bulunması çok önemlidir. Örneğin,
Hilbert (1988), ‘Matematik sanatının püf noktası, bir genellemenin bütün tohumlarını içeren
özel bir durumu bulmakta yatar.’ diye belirtmiştir.
Bu genellemeler ise matematiğin kendine özgü olan dili ile sunulur. Bu dili oluşturan
unsurlar ise, semboller, tablolar, grafikler, şekiller vb. dir. Bazı durumlarda, bu unsurların
hepsi ile genellemeler gösterilebilir. Bu nedenle, matematiğin doğasında bir simge sistemi ile
temsil edilebilen bir fikri, diğer simgelerle de temsil edebilmek ve bu simge sistemleri
arasındaki ilgiyi görebilmek de yer alır.
Bütün bunları matematikçiler nasıl yapıyor diye bir soru gelebilir. Aslında
matematikçiler genel olarak iki türlü çalışırlar. Bu gerçeği, David Tall’un birçok makalesinde
referans verdiği ünlü düşünür, matematikçi Poincaré şöyle ifade etmiştir:
Büyük matematikçilerin veya o kadarda büyük olmayan matematikçilerin çalışmalarını anlamak,
iki zıt eğilime daha doğrusu tamamen iki farklı düşünceye dikkat etmeden imkânsızdır. Bu
düşünce çeşitlerinden birisi tamamen mantıkla meşguldür, çalışmalarına baktığınızda, bunların
sanki sadece aşama aşama ilerlediklerini düşünürsünüz… hiçbir şeyi şansa bırakmadan. Diğer
düşünce çeşidindeki matematikçileri ise sezgileri yönlendirir ve bir hamlede hızlı ve büyük fetihler
gerçekleştirebilirler. [Poincaré, 1913 sayfa 210]
Poincaré sözünü ettiği farklı düşünce sistemine sahip matematikçilere örnek vermek için
Weierstrass ve Riemann’ı ele alıyor:
NEF-EFMED Cilt 2, Sayı 2, Aralık 2008 Boz, N 55
Weierstrass her şeyi serilere ve bunların analitik dönüşümlerine götürmeye çalışır; daha iyi ifade
etmek gerekirse, analizi aritmetiğin bir çeşit uzantısına indirger; bütün kitaplarını hiçbir şekle
karşılaşmadan okuyabilirsiniz. Bunun aksine Riemann, bazen geometriden faydalanır;
kavramlarının her biri, bir kere manasını yakaladıktan sonra kimsenin unutamayacağı şekillerden
ibarettir. [ibid, sayfa 212]
Fakat bu iki düşünce sistemine sahip matematikçilere örnek verirken, Poincaré tamamen
işin mantığı ile meşgul olan, diğer bir değişle analitik düşünce sistemine sahip olan
matematikçilerin kendilerine özgü sezgileri olduğunu belirtmeden geçmiyor:
... M. Hermite ile konuştuğunuzda kafanızda asla hislere hitap eden bir imaj oluşmaz. Fakat biraz
daha konuşunca en soyut kavramların bile onun için canlı bir varlık kadar somut olduğunu
görebilirsiniz. Bu kavramları göremeyebilir fakat bunlar onun için suni bir montajla birleştirilmiş
değil aksine kendi içlerinde bir düzene sahip olan prensiplerle birleştirilmiştirler. [ibid sayfa 220]
O zaman, matematikte sezgisel çalışmanın önemi büyüktür. İster analitik düşünce
sistemi, ister sezgisel düşünce sistemi baskın olsun, matematikçilerin sezgilerini kullandıkları
anlar oluyor. Bu nedenle, sezgisel düşünce sisteminin de birçok çeşidi vardır diyebiliriz:
O zaman birçok çeşit sezgiler vardır; birincisi hislere ve hayal gücüne hitap eder; sonra,
indüksiyon ile yapılan genellemeleri kapsayan sezgiler, yani deneye dayalı bilimlerin kullandığı
prosedürlerden alınan sezgisel düşünce; son olarak ta sayılardan alınan sezgilerimiz mevcuttur…
[ibid. sayfa 215]
Poincaré’ nin bahsettiği düşünme çeşitlerine Pascal’da paralel şekilde değiniyor:
sezgisel düşünme yeteneğine sahip kişiler esnektir ve aynı anda birçok şeyi ele alabilip
düşünebilir, bunun aksine analitik düşünme prensibine sahip kişiler buluşlarına çok yavaş
ulaşırlar, ama bu buluşları sağlam ve muhkem olur.
Poincaré’ nin bahsettiği sezgi türlerinden sayılarla ilgili olanı son yıllarda eğitim
camiasında yoğun ilgi çekmiştir. Hatta Dehane (2001) sayılarla ilgili sezgilerin nasıl olduğunu
kapsamlı şekilde açıkladığı bir kitap yazmıştır. Fakat şu belirtilmelidir ki Dehane bu kitabında
sayı sezgisinin sadece insanlarda olmadığını, bazı hayvanlarda da olacağını iddia etmiştir.
Örneğin kargaların ikiyi, üçü hissedebildiğini yazmıştır.
Sayı sezgisinden sonra, eğitim araştırmacılarının ortaya attığı diğer sezgi türü ise
‘sembol sezgisi’ olarak adlandırılmıştır. Arcavi (1994), sembol sezgisinin ne olduğunu
açıklarken, bu sezginin karmaşık ve çok yönü olan bir hissetme kabiliyeti olduğunu belirtiyor.
Bunu açmak için, sembol sezgisinin ne gibi unsurları olacağını şöyle açıklıyor:
Sembol sezgisi, sembollerin gücünü anlamayı ve estetik bir duyguyu kapsar. Ayrıca
semboller kullanılmadığı takdirde gösterilemeyecek ilişkileri, genellemeleri ve ispatları
göstermek için sembolleri ne zaman ve nasıl kullanılacağını öngörebilmek, problemleri
Necatibey Eğitim Fakültesi Elektronik Fen ve Matematik Eğitimi Dergisi 56 MATEMATİK NEDEN ZOR?
çözerken, sürekli sembollerin manasını kontrol etmek; sembollerin değişik durumlarda
değişik anlamlarını hissedebilmek; problemlerin çözümünde sembolik gösterimlerin işe
yaramayacağı durumları öngörebilmek gibi kabiliyetler sembol sezgisinin içinde yer alır.
Şimdiye kadar anlatılanları özetleyecek olursak, “matematik insanların evrendeki gizli
düzeni anlamaları için insanlar tarafından üretilen bir bilimdir” diyebiliriz. Bu bilim, ilişkileri
açıklarken kendine has bir dili ve sistematiği kullanır. Bu dili ve sistematiği kullanmak için,
insanın değişik düşünce türlerine sahip olması gerekir. Özellikle analitik düşünme ve sezgisel
düşünme matematiğin olmazsa olmaz düşünme prensiplerindendir. Bu fikirler, platonist ve
problem-çözme görüşünün matematiğin doğası hakkında ileri sürdüğü fikirlere yakındır.
Fakat eskiden, yeni müfredatlar uygulanmaya konulmadan önce, matematik
sınıflarımızda enstrümentalist görüşün baskısı altındaydı. Bu iddiayı kendi eğitim sürecime ve
o yıllarda basılan kitaplardan örneklere dayandırıyorum. Tamamen düşünmeye ve sezgilere
dayanan matematik, eskiden sınıflarımızda bu tür düşünce disiplinlerini kazandıracak şekilde
sunulmuyordu. Ama müfredat değişikliklerinin altında yatan amaçlar aslında bu tür düşünce
disiplinlerini kazandırma gayesi güder. Bu iddialar aşağıdaki kısımda genişçe ele alınacaktır.
Eskiden Sınıflarımızda Sunulan Matematik Derslerinin Doğası
Ülkemizde uygulamaya konulan yeni ilköğretim programlarının beslendiği kaynakları
aşağıdakileri okuyunca daha iyi anlayacağız. Genelde eğitim programlarının, özelde bu
programları sınıfta sunan öğretmenlerin matematiği algılaması ile sınıfta sunulan matematik
derslerinin doğası arasında yakın ilişkiler vardır (Beswick, 2005). Bu nedenle eskiden
sınıflarımızda sunulan matematik derslerinin doğası hakkında yorum yapmak için, öncelikle
aşağıda birbiri ile tamamen zıt iki görüşü sunmak istiyorum. Bu görüşler, batıda yeni
matematik eğitim reformları atılırken, bu reformların eski sistem ile arasındaki farkları ortaya
koymak için Davis (1992) tarafından kaleme alınmıştı. Bu görüşleri incelediğimizde, eminim
ki eskiden okullarımızda sunulan matematik derslerinin doğası ile ilgili ipuçları
bulabileceksiniz:
Tablo 1 Matematiğin Doğası Hakkındaki Görüşler
Önceki Görüş Yeni-yeni oluşan görüş
Matematik kâğıt üzerindeki sembollerden
ibarettir;
‘Matematik’ bir düşünme yoludur ki bu
problem durumlarının ve ilgili bilgilerin
akılda simgelenmesidir (mental
representation). Yazılı semboller kullanılabilir
(hatta manipulatif materyallerle gerçek
simgeler kullanılabilir), fakat işin esası
NEF-EFMED Cilt 2, Sayı 2, Aralık 2008 Boz, N 57
öğrencinin aklında neler gerçekleştiğidir.
Matematik bilgisi kelime ve cümlelerden
oluşturulur ( ve bunlar özellikle neyi nereye
yazacağımızı söyleyen kurallarla ilgili
cümlelerdir);
Bu önemli akıl simgeleri daha öncelerden
öğrenilmiş parçalardan oluşturulur. Bu
genellikle somut deneyimlerdir, fakat her
zaman böyle olması gerekmez… Akıl
simgeleri çoğu zaman yazılı semboller
değildir, fakat bu sembollerle neler temsil
edildiğidir. 2.15 lik uzun bir adamın akıldaki
temsili asıl olarak ‘7’ rakamı değildir, 4
harften oluşan ‘adam’ kelimesi değildir, fakat
çok uzun bir insanoğludur (beklide bir
basketbol oyuncusudur).
Akıl simgelerinin oluşturulmasına kelimeler
yardımcı olabilir, ama bu demek değildir ki bu
simgelerin kendileri kelimelerden oluşsun.
(Eğer, ‘köpek’ dersem, sizin aklınıza bir şey
gelebilir, fakat çoğu zaman bu beş harfli
‘köpek’ kelimesi olmaz…)
Matematik öğretmek öğrencilere doğru yere doğru
şeyleri yazmayı öğretmektir;
‘Matematiği öğretmek’ öğrencilerin temel
yapı taşlarından oluşan dağarcıklarını
kendilerinin geliştirmesine mihmandarlık ve
kılavuzluk yapmak ve öğrencilerin akıl
simgelerini oluşturup kullanma kabiliyetlerini
geliştirmeye yardımcı olmak meselesidir.
Matematiği öğrenmenin amacı birkaç kuralı
ezberlemektir (örneğin 3 kere 4 = 12), sembollerin
kâğıt üzerinde manipülasyonları için birkaç
standart algoritma ve birkaç tanımı öğrenmek
yeterlidir. İleri matematiğin püf noktası da birkaç
ispatı ezberlemekten geçer. Her halükarda, amaç
kabul edilmiş emirlere uymaktır – öğrenciler
standart algoritmaları doğru şekilde, doğru yerlere
yazmalıdır.
Matematik çalışmanın amacı, yukarıda
anlatıldığı gibi düşünme yollarını öğrenmedir.
Öğrenciler, algoritmaları kendileri icat edemezler.
Öğrenciler çoğu zaman kendi algoritmalarını
kendileri icat ederler, fakat bunu genellikle
yetişkinlere bildirmezler, çünkü büyük ihtimal
bu algoritmaları kabul görmez.
‘Değerlendirme’ öğrencilerin kabul görmüş
emirlere ne kadar uyduğunu ölçmektir. Bu da
onlara belli bazı standart hesaplamaları
‘Değerlendirme’ veya ‘Kanaat Oluşturma’ bir
öğrencinin ilginç problemler hakkında neler
düşündüğünü bulmaktır. Çoğu kez,
Necatibey Eğitim Fakültesi Elektronik Fen ve Matematik Eğitimi Dergisi 58 MATEMATİK NEDEN ZOR?
yapmalarını sorarak bulunabilir. Öğrencinin
gerçekte hangi yolu kullandığı önemli değildir,
önemli olan doğru sonuca ulaşıp ulaşmadığıdır.
öğrencilere alışılmamış problemleri
çözdürmek ve onların bunu çözmede nasıl bir
yol izlediğini gözlemlemek daha öğreticidir.
Sıklıkla, problem üzerinde çalışırlarken,
öğrencilerden sesli düşünmeleri istenir,
böylece problem hakkında neler
düşündüklerini ve nedenlerini (ellerinden
geldiğince) anlamamıza yardımcı olurlar.
Yukarıdaki listedeki görüşleri incelediğimizde, eski görüşün müfredat değişikliğinden
önce okullarımızda etkin olduğunu düşünmemek elde değil. Gerçekten, öğrencilerimize
matematiği sembollerin kâğıt üzerinde nasıl oynatılacağını öğretiyorduk. Bunun için, onlara
oyunun kurallarını üzerine basa basa tahtaya yazıp, sözle ifade ediyorduk. Bu kuralları
ezberleyip tekrarlamaları için onlara alıştırma kâğıtları hazırlıyorduk. Bunlar, genelde gerçek
hayattan kopuk, amacı sadece sembol manipülasyonunun kurallarını vurgulayan sorulardan
oluşuyordu. Bunun sebebi öğrencilerimizi her an bekleyen seçme sınavlarına hazırlamak
olabilir. Bu sınavlar zamana karşı yapıldığından, çocuklarımıza kuralları en kolay nasıl
ezberleyip ve en kolay nasıl geri çağrılacağını öğretmek zorunda kalmış olabiliriz.
Bunları daha da açmak için Skemp (1976)’in 1970li yıllarda, İngiltere’ deki okullarda
sunulan matematik derslerinin doğasını açıkladığı örnekleri sunmak istiyorum. Göreceksiniz
ki, o yıllarda, İngiliz okullarındaki durum, yeni müfredatların uygulanmasından önce bizim
okullarda yaşanan duruma çok benziyor.
Ders işlenirken, öğretmen sınıfa üçgenin alanını Alan=
( )
1
2
A⋅ B
formülü verir diye bir
hatırlatma yapıyor. Önceki dersleri kaçırmış bir öğrenci anlamadım hocam diyor.
Öğretmende, bu kuralı değişik bir şekilde tekrarlıyor: ‘Bu formül size üçgenin alanının nasıl
bulunacağını söylüyor; yani taban ile yüksekliği çarpıp, ikiye böleceksiniz.’ Bunun üzerine
öğrenci: ‘Ha tamam, anladım’ deyip, alıştırmalara devam ediyor. Biz bu öğrenciye: ‘Anladım
diyorsun, ama aslında anlamadın.’ desek, öğrenci: ‘Elbette anladım, bakın bütün bu
alıştırmaları doğru yaptım’ diyerek itiraz edebilir. Belki de, anlamadın demekle onu
küçümsediğimizi zannederek, morali bozulabilir. Gerçekten, o öğrenci kendine göre
anlamıştır; çünkü onun anlamaya verdiği mana alıştırmaları doğru çözmekten geçiyor.
Bu tür örneklerden hepimiz bulabiliriz: çıkarmada ‘eldeyi’ unutma, kesirleri bölerken
sağdakini ters çevir, denklemlerde işaret değiştirmeyi unutma gibi kural hatırlatmaları en
NEF-EFMED Cilt 2, Sayı 2, Aralık 2008 Boz, N 59
bariz örneklerdendir. Eski ders kitaplarına bakılırsa onlarda da bu türden kural ezberletmeye
yönelik hatırlatmalar görülebilir. Örneğin aşağıda ki örnekler, okullarımızda kullanılan, eski
ders k
ri toplanır,
ade, çok terimli bir ifade ile çarpılırken; tek terimli, çok terimlinin her terimi ile ayrı
k için, bölünen sayı, bölenin çarpmaya göre tersi ile çarpılır.
e işlemi sürdürülür.
terimlerini kullanıyor.
Bu ya
rden geldiğini anlamak zordur. Ama bu kural ezberlenince birçok
k hoştur ve
irdeleyerek çalışan matematikçiler, bazen
itaplarından alınmıştır:
Harfli ifadelerle çarpma
Harfli ifadeler çarpılırken kat sayılar çarpılır, kat sayı olarak yazılır. Aynı harflerin üsle
o harfe üs olarak yazılır. Tabanı aynı olmayan harfli ifadeler ise aynen çarpıma yazılır.
Tek terimli if
ayrı çarpılır.
Rasyonel Sayılar kümesinde bölme İşlemi
Bir rasyonel sayıyı diğerine bölme
Ondalık kesirlerle bölme işlemi
Bir ondalık kesri bir sayma sayısına bölerken, virgül dikkate alınmadan bölm
Sıra kesir kısmına gelince bölüme virgül konup, bölme işlemine devam edilir.
Okuyucuyu, okul hayatlarından veya eski matematik ders kitaplarından buna benzer,
kural ezberletmeye yönelik örnekler bulmaya davet ediyorum. Biraz düşününce, göreceğiz ki
okullarımızda kuralların nerden, nasıl geldiğini ve bunların birbiri ile ilgilerini kavratmaktan
çok, öğrencilerimize uymaları gereken kurallar dizisini ezberletmeye çalışıyorduk. Bu
birbirine zıt iki öğretim yaklaşımını açıklamak için Skemp (1976), kuralları ezbere dayalı
‘instrumental’ ve bağlantıları anlamaya dayalı ‘relational’ matematik
klaşımların avantajlarını, Skemp (1976) aşağıdaki gibi listeliyor.
Kuralları ezbere dayalı matematik öğretiminin avantajları şöyle sıralanabilir:
1. Çoğu kez daha kolay anlaşılır; bazen çok daha kolay olur. ‘Eksi çarpı eksi
eşittir artı’ kuralının ne
soru kolayca çözülür.
2. Bu nedenle ezbere dayalı matematik öğreniminin semeresi daha kısa zamanda
ve açık olarak görülür. Sayfalar dolusu soruyu doğru cevaplamak ço
öğrencilerin bu tür başarılardan duydukları hazzı küçümsememek gerekir.
3. Sorular daha kısa yoldan ve güvenilir şekilde kuralları ezberleyerek çözülür.
Gerçekten bazen matematikçiler bile kuralları ezberleyip kullanabilir. Yani, çoğu zaman
kuralların nedenlerini ve birbiri ile ilgilerini
kuralları ezbere kullanarak soruları çözebilir.
Necatibey Eğitim Fakültesi Elektronik Fen ve Matematik Eğitimi Dergisi 60 MATEMATİK NEDEN ZOR?
Skemp (1976) kuralları ezberleyerek öğretilen ve öğrenilen matematiğin avantajlarından
ancak bu kadarını sayıyor ve eğer daha başka avantajları varsa bunları öğrenmekten mutluluk
içinde kullanırsa geriye kalan soruları yanlış bulmuş olur. Hangi soruda
alanlarını bulmada kullanılan formüllerin
ı
erini irdelemeden duyulan haz, kişiyi yeni alanları
duyacağını yazıyor.
Skemp (1976) bağlantıları anlamaya dayalı matematik öğretiminin en az 4 tane
avantajını şu şekilde listeliyor:
1. Bilgilerin yeni, alışılmamış durumlara adaptasyonu daha kolaydır. Örneğin,
kuralları ezberleyerek öğrenen bir öğrenci, üçgende verilmeyen açıyı, verilen iki açının
toplamını bulup, bunu 180’den çıkar kuralını uygulayarak bulabilir. Bu kuralı
kullanarak soruların %80’nini doğru cevaplayabilir. Ama bu öğrenci, aynı kuralı bir dış
açıyı bulmak
hangi kural çalışacağını bilmenin yanında o kuralın neden orada çalışacağını bilmek,
kişiye alışılmamış problemlerde bu kuralı kullanıp yeni kurallar keşfetmesini
sağlayabilir.
2. Hatırlanması daha kolaydır. Burada bir çelişki hissedebilirsiniz. Fakat şu
belirtilmelidir ki, kuralların, kavramların arasındaki ilgi gözetilerek, nedenleri
irdelenerek öğrenmek zor olduğundan, bunların unutulması da zordur. Mesela, denk
kesirler, kesirleri sadeleştirme ve genişletme, kesirleri toplamak birbiri ile ilgili
konulardır. Bu kavramlar, aralarındaki ilgi gösterilerek öğretilirse, bir kavramı bilen
diğer kavramı öğrenirken zorluk çekmez. Aynı şekilde, üçgenlerin, dikdörtgenlerin,
karelerin, paralelkenarların, yamukların
arasındaki ilgiler vurgulanırsa, her biri için ayrı formül ezberlenmek zorunda kalınmaz.
Bu nedenle bir formülü nedenleri ile bilen kişi bunu kolayca hatırlayıp bütün bu
şekillerin alanlarını bulmada kullanabilir.
3. Nedenleri ve bağlantıları anlamaya çalışmak motivasyonu artırır. Bu avantaj
birçok araştırma göstermiştir. Bu yaklaşım kullanılarak işlenen matematik derslerinde,
öğrenciler dışarıdan gelecek ödül veya cezalara pek ihtiyaç duymazlar. Bu tür çalışma
kişiye büyük haz verir. Bu da öğretmenin işini ‘motivasyon’ bağlamında kolaylaştırır.
4. Kuralların nedenini incelemek yeni matematiksel bilginin gelişimini
kolaylaştırır. Bu fayda, aslında, bir önceki avantajdan çıkarılabilir. Yani, kuralların
nedenlerini ve birbiri ile ilgil
incelemeye iter. Bu alanlar incelenirken, yeni materyaller öğrenilir. Bu durumu bir
ağacın köklerini geliştirmesine veya bir hayvanın yiyecek bulması için yeni bölgelere
keşfe çıkmasına benzetebiliriz.
NEF-EFMED Cilt 2, Sayı 2, Aralık 2008 Boz, N 61
Yukarıda avantajlarını sunulan matematik öğretimine veya öğrenimine yaklaşımlar
gösteriyor ki, eskiden okullarımızda matematik dersleri genelde kuralları ezbere dayalı bir
yaklaşımla sunuluyordu. Bu tür yaklaşımın avantajlarının bizim eğitim sistemimizin
ihtiyaçlarını karşılayacak türden olması, kuralların nedenleri ve birbiri ile ilişkileri
irdelenmeden sunulmasını gerektirebilir. Eğitim sisteminden kastım, yüklü müfredatlar ve
seçme sınavlarıdır. İlkokuldan liseye bütün matematik müfredatları haddinden fazla konularla
yoğunlaştırılmıştı. Bu nedenle, bu konularda kavramların gerçek hayatla ilgisi kurularak,
kuralların nedenleri ve birbiri ile ilgileri araştırılarak sunulması neredeyse imkânsız hale
getirilmişti. Sonuç olarak denebilir ki eski müfredat matematik eğitimini bir kısır döngü içine
hapsetmiştir. Kurallar ezberlenerek yetişen nesiller, kendilerinden sonra ki nesillere de aynı
yaklaşımı sunmak zorunda kalmıştır. Hatta yeni müfredat baz alınarak yetiştirilen öğretmen
adayları bile bu kısır döngüden muzdariptir. Örneğin, okullarda staj derslerine giden lise
öğretmen adayı öğrencilerimizin şikâyet ettiği konulardan biri: ‘Hocam, biz fakültede birçok
eğitim teorisi öğreniyoruz. Ama bunları staj yaptığımız okullarda uygulamamız neredeyse
imkânsız, çünkü en başta öğrenciler bizim uygulamak istediğimiz yaklaşıma yabancı, ikincisi
öğretmenler yabancı, üçüncüsü veliler yabancı. Biz yeni yaklaşım uygulayacak olsak, staj
ikâyet edecek, çocuklarımızı sınavlara
hazırlam
öğretmenimiz kesin kötü not verecek. İkincisi, veliler ş
ıyorsunuz diye.’ Bütün bunlar gösteriyor ki, köklü bir eğitim anlayışı reformuna
ihtiyacımız var.
Kaynakça
, M., Memnun, D. S ve Yazgan, Y. (2007). Sınıf Öğretmeni Adaylarının Rutin Olmayan
Matematiksel Problemleri Çözme Becerileri ve Bu Konudaki Düşü
Altun
nceleri, İlköğretim
Arcav sense-making in formal mathematics. For the
Barna
onference for the Psychology of
Besw defined contexts.
Boz, . VI. Ulusal Fen Bilimleri
Davis, R. B. (1992). Understanding “Understanding”, Journal of Mathematical Behaviour,
Ernes est (Ed.),
Fisher, R. C. & Ziebur, A. D. (1965). Calculus and Analitic Geometry Second Edition.
Gardner, H. (1993). Frames of Mind: The theory of multiple intelligence Second Edition.
Gray, of
Hilbert, D. (1988). In N. Rose , (Ed.), Mathematical Maxims and Minims, Raleigh NC: Rome
Işıksa
.
. [Online]: http://ilkogretim-online.org.tr
Online, 6(1), 127-143, 2007. [Online]: http://ilkogretim-online.org.tr
i, A. (1994). Symbol sense: Informal
Learning of Mathematics, 14(3), 24-3.
rd, T. & Tall, D. O. (1997). Cognitive Units, Connections, and Mathematical Proof. In
E. Pehkonen, (Ed.), Proceedings of the 21st Annual C
Mathematics Education, Vol. 2. Lahti, Finland, 41–48.
ick, K. (2005). The Beliefs/Practice connection in broadly
Mathematics Education Research Journal, 17, 2, 39-68.
N. (2004). Sembol Sezgisi, Bağ Kurma ve Zihinde Resmetme
ve Matematik Eğitimi Kongresi, 9 – 11 Eylül 2004, İstanbul
11, 225- 241.
Dehane, S. (2001). The Number Sense. London: Penguin Books.
t, P. (1989). The impact of beliefs on the teaching of mathematics. In P. Ern
Mathematics teaching: The state of the art (pp. 249–253). New York: Falmer.
Prentice Hall.
Fontana Press.
E. M. & Tall, D. O. (1994). Duality, ambiguity and flexibility: a proceptual view
simple arithmetic. Journal of Research in Mathematics Education, 26 (2), 115–141.
Hardy, G. H. (1941). A Mathematician's Apology, London: Cambridge University Press,.
Press Inc.
l, M., Kurt, G., Doğan, O. Ve Çakıroğlu, E. (2007). İlköğretim Matematik Öğretmen
Adaylarının Epistemolojik Kavramlamaları: Üniversite ve Sınıf Düzeyinin Etkisi
İlköğretim Online, 6(2), 313-321, 2007
MacHale, D. (2002). Wisdom. Mercier Pres.
NEF-EFMED Cilt 2, Sayı 2, Aralık 2008 Boz, N 65
Necatibey Eğitim Fakültesi Elektronik Fen ve Matematik Eğitimi Dergisi
Poinc k:
ersity Press of America edition, 1982).
Skem al understanding and instrumental understanding. Mathematics
Tall, t of the
Tall,
l reference to limits and continuity, Educational Studies in Mathematics, 12, 151-
Thurs in mathematics. Bulletin of the American
URL //iogm.meb.gov.tr/files/io1-5sinifprogramlaritanitimkit.pdf
Pascal, B. (1653). Discours sur les passions de l'amour.
aré, H. (1913). The Foundations of Science (translated by Halsted G.B.), New Yor
The Science Press, (page references as in Univ
Poisson, S. (1991). Mathematics Magazine, 64(1).
Rényi, A., & Turán, P. (1970). The Work of Alfréd Rényi. Matematikai Lapok, 21, 199 - 210.
p, R. R. (1976) Relation
Teaching, 77, 20 - 26.
Sylvester, J.J. (1869). Presidential Address to British Association.
D. O., & M. Thomas, G. Davis, E. Gray, A. Simpson. (2000). What is the objec
encapsulation of a process?, Journal of Mathematical Behavior, 18 (2), 1-19.
D. O., & Vinner, S. (1981). Concept image and concept definition in mathematics, with
specia
169.
ton W. P. (1990). On proof and progress
Mathematical Society, 30(2), 161-177.
1: http: , erişim 22 Ekim
URL 2. http://timss.bc.edu./timss2003i/mathD.html
2008.
erişim 20 Ocak 2006.
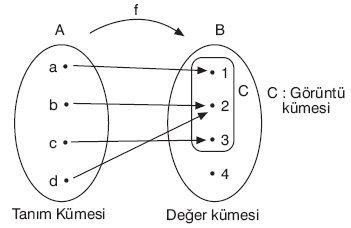
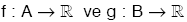 fonksiyonları tanımlansın.
fonksiyonları tanımlansın. , (f + g)(x) = f(x) + g(x)
, (f + g)(x) = f(x) + g(x) , (f – g)(x) = f(x) – g(x)
, (f – g)(x) = f(x) – g(x) , (f × g)(x) = f(x) × g(x)
, (f × g)(x) = f(x) × g(x)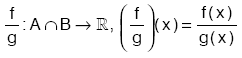
 olmak üzere,(c × f) : A ®
olmak üzere,(c × f) : A ® , (c × f)(x) = c × f(x) tir.
, (c × f)(x) = c × f(x) tir.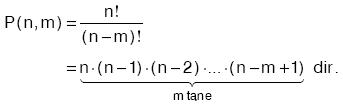
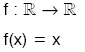
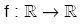
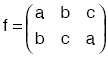 biçiminde gösterilir.
biçiminde gösterilir.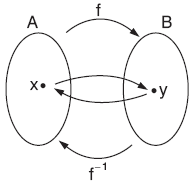
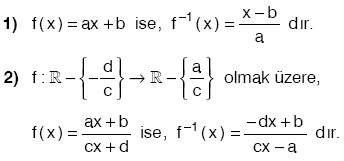
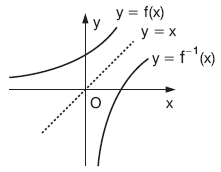
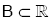 olmak üzere,
olmak üzere,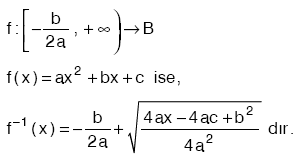
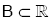 olmak üzere,
olmak üzere,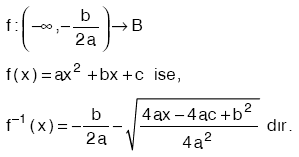
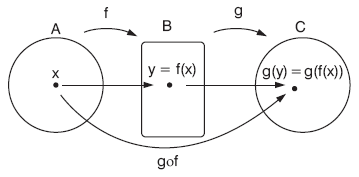
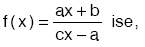













.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)


.jpg)


.png)












.jpg)
.jpg)