FONKSİYON
A. TANIM
A ¹ Æ ve B ¹ Æ olmak üzere, A dan B ye bir b bağıntısı verilmiş olsun.
A nın her elemanı B nin elemanlarıyla en az bir kez ve en çok bir kez eşleniyorsa bu bağıntıya fonksiyon denir.
A nın her elemanı B nin elemanlarıyla en az bir kez ve en çok bir kez eşleniyorsa bu bağıntıya fonksiyon denir.
“x Î A ve y Î B olmak üzere, A dan B ye bir f fonksiyonu
f : A ® B ya da x ® f(x) = y biçiminde gösterilir. A ya fonksiyonun tanım kümesi, B ye dedeğer kümesi denir.
f : A ® B ya da x ® f(x) = y biçiminde gösterilir. A ya fonksiyonun tanım kümesi, B ye dedeğer kümesi denir.
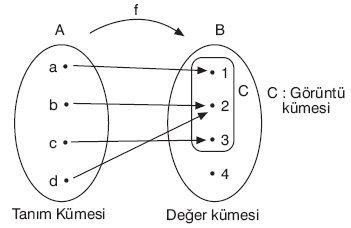
Yukarıda A dan B ye tanımlanan f fonksiyonu
f = {(a, 1), (b, 2), (c, 3), (d, 2)}
biçiminde de gösterilir.
| Ü | Her fonksiyon bir bağıntıdır. Fakat her bağıntı fonksiyon olmayabilir. |
| Ü | Görüntü kümesi değer kümesinin alt kümesidir. |
| Ü | s(A) = m ve s(B) = n olmak üzere,
i) A dan B ye nm tane fonksiyon tanımlanabilir.
ii) B den A ya mn tane fonksiyon tanımlanabilir.
iii) A dan B ye tanımlanabilen fonksiyon olmayan bağıntıların sayısı 2m × n – nm dir.
|
| Ü | Grafiği verilen bir bağıntının fonksiyon olup olmadığını anlamak için, y eksenine paralel doğrular çizilir. Bu doğrular fonksiyonun belirttiği eğride en az bir ve en çok bir noktayı kesiyorsa verilen bağıntı x ten y ye bir fonksiyondur. |
B. FONKSİYONLARDA İŞLEMLER
A Ç B ¹ Æ olmak üzere,
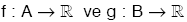 fonksiyonları tanımlansın.
fonksiyonları tanımlansın.- (f + g) : A Ç B ®
 , (f + g)(x) = f(x) + g(x)
, (f + g)(x) = f(x) + g(x) - (f – g) : A Ç B ®
 , (f – g)(x) = f(x) – g(x)
, (f – g)(x) = f(x) – g(x) - (f × g) : A Ç B ®
 , (f × g)(x) = f(x) × g(x)
, (f × g)(x) = f(x) × g(x) - “x Î A Ç B için, g(x) ¹ 0 olmak üzere,
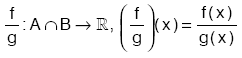
- c Î
 olmak üzere,(c × f) : A ®
olmak üzere,(c × f) : A ® , (c × f)(x) = c × f(x) tir.
, (c × f)(x) = c × f(x) tir.
C. FONKSİYON ÇEŞİTLERİ
1. Bire Bir Fonksiyon
Bir fonksiyonda farklı elemanların görüntüleri de farklıysa fonksiyon bire birdir..
BBuna göre, bire bir fonksiyonda,
“x1, x2 Î A için, x1 ¹ x2 iken f(x1) ¹ f(x2) olur.
Diğer bir ifadeyle,
“x1, x2 Î A için, f(x1) = f(x2) iken
x1 = x2 ise, f fonksiyonu bire birdir.
| Ü | s(A) = m ve s(B) = n (n ³ m) olmak üzere,
A dan B ye tanımlanabilecek bire bir fonksiyonların sayısı,
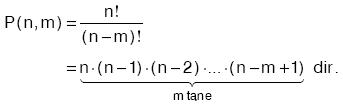 |
2. Örten Fonksiyon
Görüntü kümesi değer kümesine eşit olan fonksiyonlara örten fonksiyon denir.
| Ü | f : A ® B
f(A) = B ise, f örtendir.
|
| Ü | s(A) = m olmak üzere, A dan A ya tanımlanabilen bire bir örten fonksiyonların sayısı,
m! = m × (m – 1) × (m – 2) × … × 3 × 2 × 1 dir.
|
3. İçine Fonksiyon
Örten olmayan fonksiyona içine fonksiyon denir.
| Ü | İçine fonksiyonun değer kümesinde eşlenmemiş eleman vardır. |
| Ü | s(A) = m olmak üzere, A dan A ya tanımlanabilen içine fonksiyonların sayısı mm – m! dir. |
4. Birim (Etkisiz) Fonksiyon
Her elemanı kendisine eşleyen fonksiyona birim fonksiyon denir.
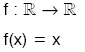
ise, f birim (etkisiz) fonksiyondur.
| Ü | Birim fonksiyon genellikle I ile gösterilir. |
5. Sabit Fonksiyon
Tanım kümesindeki bütün elemanları değer küme-sindeki bir elemana eşleyen fonksiyonasabit fonksiyon denir.
| Ü | “x Î A ve c Î B için,
f : A ® B
f(x) = c
ise, f sabit fonksiyondur.
|
| Ü | s(A) = m, s(B) = n olmak üzere,
A dan B ye n tane sabit fonksiyon tanımlanabilir.
|
6. Çift ve Tek Fonksiyon
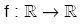
f(–x) = f(x) ise, f fonksiyonu çift fonksiyondur.
f(–x) = –f(x) ise, f fonksiyonu tek fonksiyondur.
| Ü | Çift fonksiyonların grafikleri Oy eksenine göre simetriktir. |
| Ü | Tek fonksiyonların grafikleri orijine göre simetriktir. |
D. EŞİT FONKSİYON
f : A ® B
g : A ® B
Her x Î A için f(x) = g(x) ise, f fonksiyonu g fonksiyonuna eşittir.
E. PERMÜTASYON FONKSİYON
f : A ® A
olmak üzere, f fonksiyonu bire bir ve örten ise, f fonksiyonuna permütasyon fonksiyon denir.
A = {a, b, c} olmak üzere, f : A ® A
f = {(a, b), (b, c), (c, a)}
fonksiyonu permütasyon fonksiyon olup
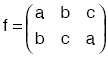 biçiminde gösterilir.
biçiminde gösterilir.
F. TERS FONKSİYON
f : A ® B, f = {(x, y)|x Î A, y Î B} bire bir ve örten fonksiyon olmak üzere,
f–1 : B ® A, f–1 = {(y, x)|(x, y) Î f} fonksiyonuna f nin ters fonksiyonu denir.
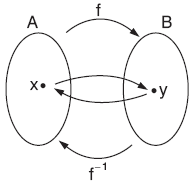 | (x, y) Î f ise, (y, x) Î f–1 olduğu için,
y = f(x) ise, x = f–1(y) dir.
Ayrıca, (f–1)–1 = f dir.
|
| (f–1)–1 = f dir. Ancak, (f–1(x))–1 ¹ f(x) tir. |
| f fonksiyonu bire bir ve örten değilse, f–1 fonksiyon değildir. |
| f : A ® B ise, f–1 : B ® A olduğu için, f nin tanım kümesi, f–1 in değer kümesidir. f nin değer kümesi de, f–1 in tanım kümesidir. |
| f(a) = b ise, f–1(b) = a dır.
f–1(b) = a ise, f(a) = b dir.
|
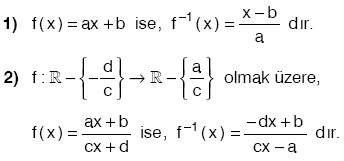 |
| Ü | y = f(x) fonksiyonunun grafiği ile y = f–1(x) in grafiği y = x doğrusuna göre birbirinin simetriğidir. 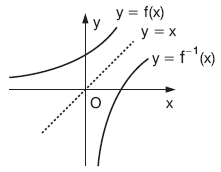 |
| Ü | 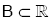 olmak üzere, olmak üzere,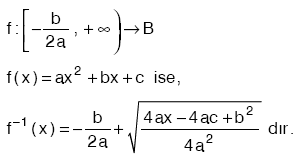 |
| Ü | 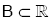 olmak üzere, olmak üzere,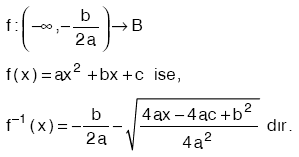 |
G. BİLEŞKE FONKSİYON
f : A ® B, g : B ® C fonksiyonları tanımlansın.
f ve g yi kullanarak A kümesinin elemanlarını C kümesinin elemanlarına eşleyen fonksiyona g ile f nin bileşke fonksiyonu denir.
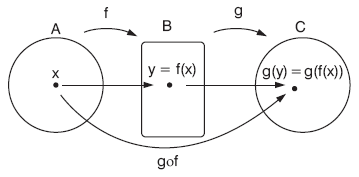
Buna göre,
f : A ® B ve g : B ® C olmak üzere, gof : A ® C fonksiyonuna f ile g nin bileşke fonksiyonu denir ve g bileşke f diye okunur.
| Ü | (gof)(x) = g[f(x)] tir. |
| Bileşke işleminin değişme özeliği yoktur.
Bu durumda, fog ¹ gof dir.
Bazı fonksiyonlar için fog = gof olabilir. Ancak bu “fonksiyonlarda değişme özeliği yoktur.” gerçeğini değiştirmez.
|
| Ü | Fonksiyonlarda bileşke işleminin birleşme özeliği vardır.
Bu durumda (fog)oh = fo(goh) = fogoh olur.
|
| Ü | I birim fonksiyon olmak üzere,
foI = Iof = f ve
f–1of = fof–1 = I dır.
|
| Ü | f, g ve h fonksiyonları bire bir ve örten olmak üzere,
(fog)–1 = g–1of–1 ve
(fogoh)–1 = h–1og–1of–1 dir.
|
| Ü | (fog)(x) = h(x)
ise, f(x) = (hog–1)(x) dir.
ise, g(x) = (f–1oh)(x) tir.
|
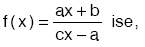
• f–1 (x) = f(x) tir.
• (fof) (x) = x
• (fofof) (x) = f(x)
• (fofofof) (x) = x
…
|
H. FONKSİYONUN GRAFİĞİ
Bir fonksiyonun elemanlarına analitik düzlemde karşılık gelen noktaların kümesine bu fonksiyonun grafiği denir.
f : A ® B, f = {(x, y)|x Î A, y Î B, y = f(x)}
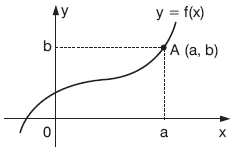 | (a, b) Î f
olduğundan
f(a) = b dir.
Ayrıca, f–1(b) = a dır.
|
| Ü | 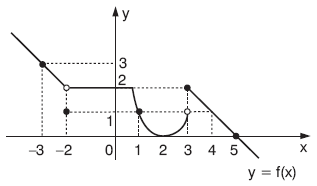
Yukarıdaki y = f(x) fonksiyonunun grafiğine göre,
f(–3) = 3, f(–2) = 1, f(–1) = 2, f(0) = 2, f(1) = 1,
f(2) = 0, f(3) = 2, f(4) = 1, f(5) = 0 dır.
|
Fonksiyonlar – Konu Anlatımı ve Soru Çözümü
YanıtlaSilLise hayatınızdan itibaren matematik dersini zorlaştıran, özellikle çok fazla çalışmayan öğrenciler için bela olan ve neredeyse her türlü alanda karşımıza çıkan fonksiyonlar konusunu işleyeceğiz. TYT Matematik fonksiyonlar konu anlatımı içeriğine baktığımızda ayt kısmına nazaran daha az, daha basit ve daha anlaşılabilir içerikler ile karşılaşacağız. Fakat ilkokulda öğrendiğiniz sayısal konularından sonra böyle bir olgu sizi biraz...
fonksiyonlar konu anlatımı